g/l💖a:~🌈 cat xenharmonic-pdxwlf-26
Xenharmonic Lights and Music
Grid keyboard
Violin layout
Kite tuning layout
Halberstadt piano 72edo layout
Mosaichord
Description
This installation combines lights and music to help guide people through a musical journey inspired by the past, present, and future of tuning.
While the piano is old and familiar, the notes on this piano keyboard are tuned in a way much older than standard 12edo tuning. These ancient notes can also be found on two modern microtonal keyboards made here in Portland. The colors of lights are visual aids to translate between 3 different keyboards. The key grid can switch to different layouts.
The colors of the keys represent their closest and most obvious frequency ratio prime factors. Primes 2 and 3 are white. 3 is called Pythagorean tuning. Prime 5 is yellow and green. Prime 7 is blue and red. Exploring primes 2-7 is a gateway to higher primes 11, 13, 17, and 19. Not only have these notes been loved through ancient times, they are foundational to music synthesis and perception.
Standard Halberstadt piano
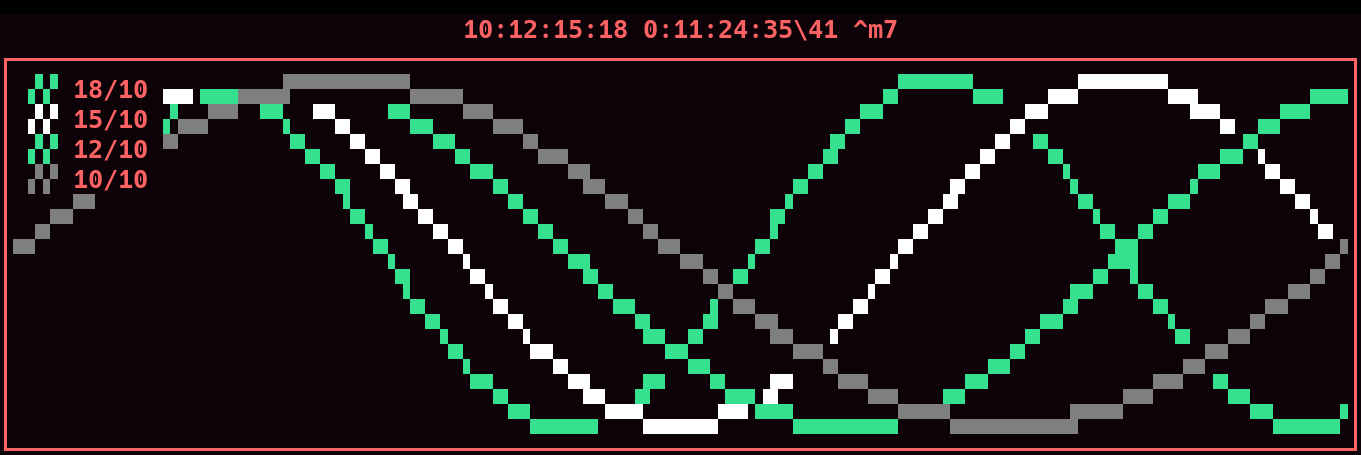
Prime 5 is different than prime 3 by not tempering 81/80.
2/1 C 2/ P8 41\41
15/8 vB 5/ vM7 37\41
9/5 ^Bb /5 ^m7 35\41
5/3 vA 5/ vM6 30\41
8/5 ^Ab /5 ^m6 28\41
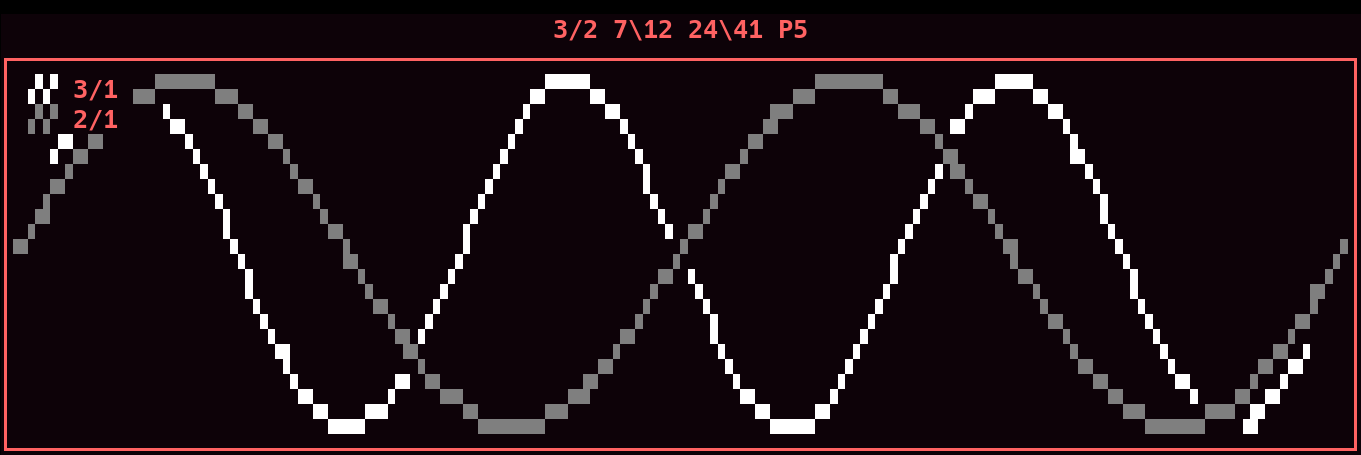
3/2 G 3/ P5 24\41
64/45 ^Gb /5 ^d5 21\41
4/3 F /3 P4 17\41
5/4 vE 5/ vM3 13\41
6/5 ^Eb /5 ^m3 11\41
9/8 D 3/ M2 7\41
16/15 ^Db /5 ^m2 4\41
1/1 C P1 0\41
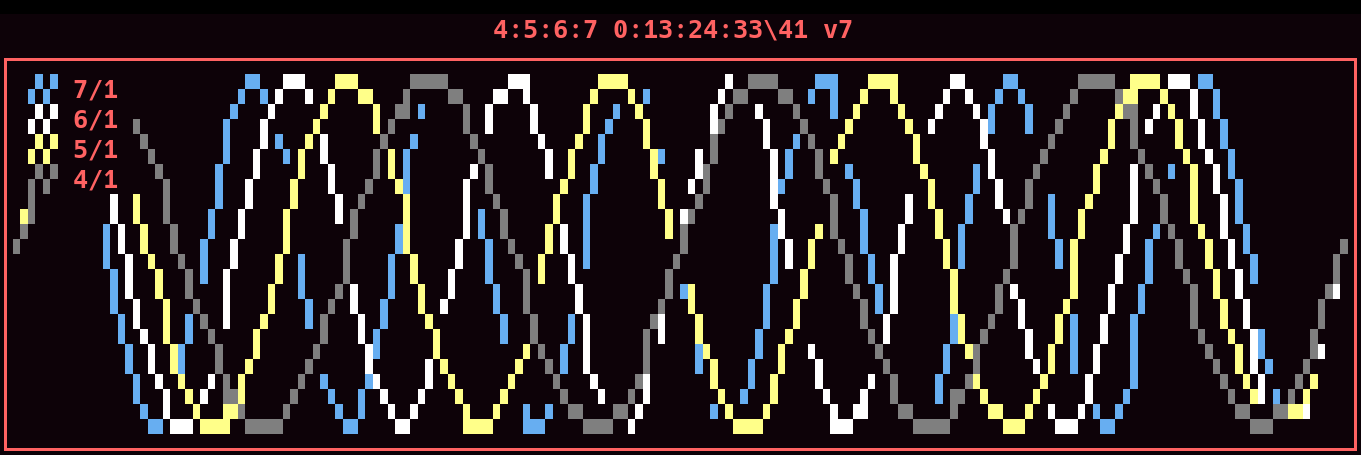
Prime 7 is coming from prime 5 by tempering 225/224.
2/1 ^Db 2/ P8 41\41
15/8 C 5/ vM7 37\41
7/4 vB 7/ vm7 33\41
27/16 ^Bb 3/ M6 31\41
14/9 vA 7/ vm6 26\41
3/2 ^Ab 3/ P5 24\41
45/32 G 5/ vA4 20\41
4/3 ^Gb /3 P4 17\41
5/4 F 5/ vM3 13\41
7/6 vE 7/ vm3 9\41
9/8 ^Eb 3/ M2 7\41
135/128 D 5/ vA1 3\41
1/1 ^Db P1 0\41
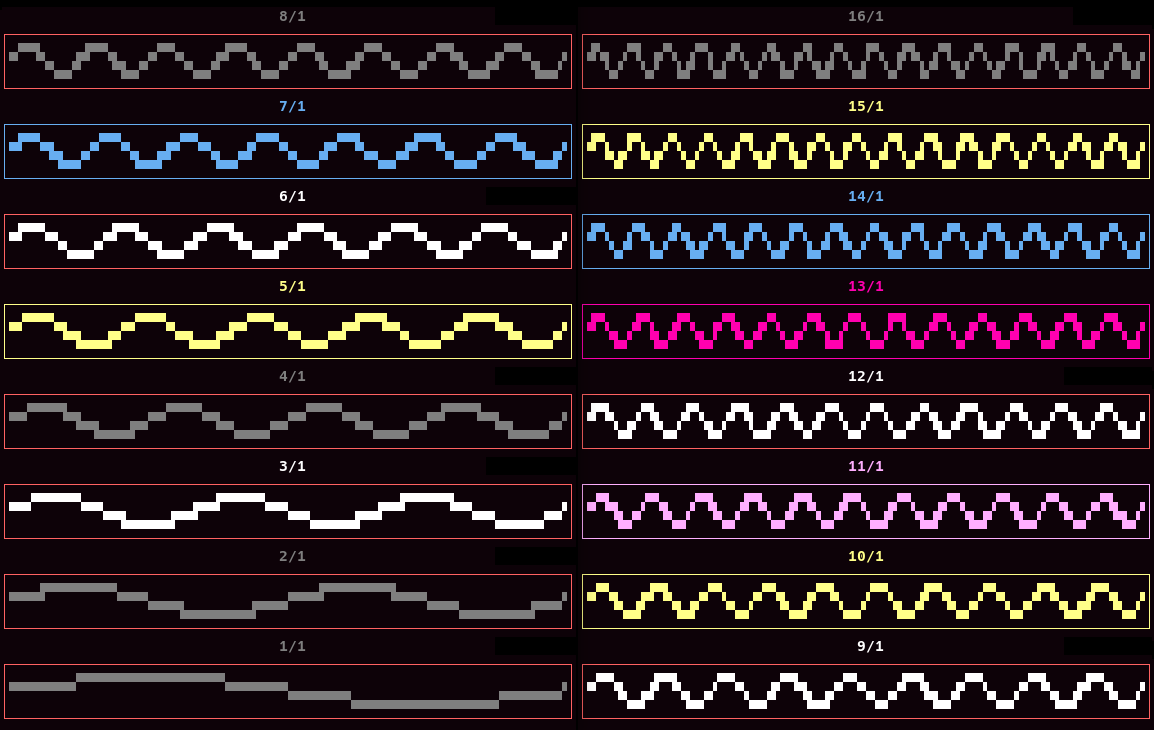
Harmonic Series: Ancient Music Technology
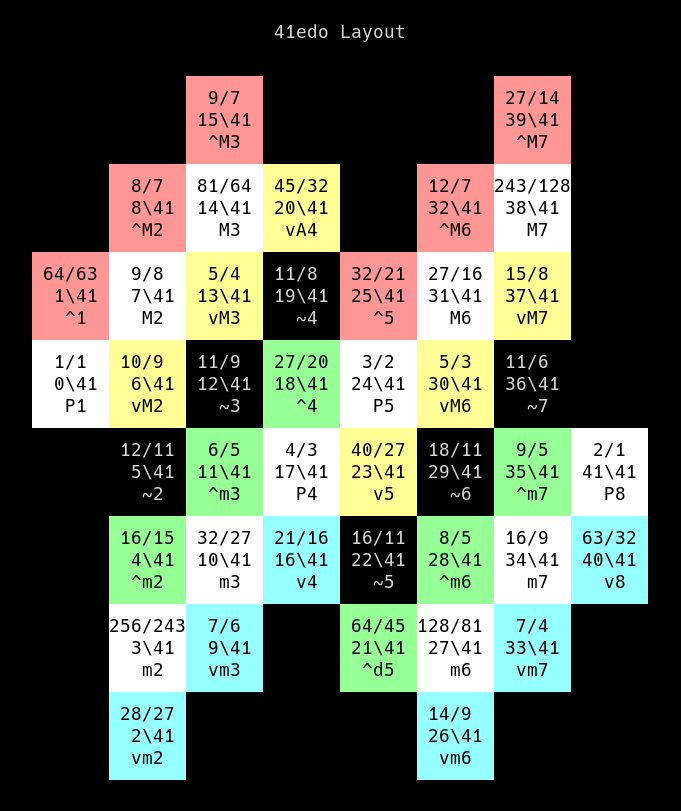
41edo 3rds
^M3 9/7 high prime: /7 underM3 81/64 high prime: 3/ over
vM3 5/4 high prime: 5/ over
~3 11/9 high prime: 11/ over
^m3 6/5 high prime: /5 under
m3 32/27 high prime: /3 under
vm3 7/6 high prime: 7/ over
Run this in the terminal to factor 81/64 and 32/27.
g/l💖a:~🌈 factor 81 64
81: 3 3 3 3
64: 2 2 2 2 2 2
g/l💖a:~🌈 factor 32 72
32: 2 2 2 2 2
27: 3 3 3
Run this in the python shell to see powers of 2 and 3. This is the inverse of above which shows prime factors.
g/l💖a:~🌈 python3
Python 3.8.5 (default, Jul 28 2020, 12:59:40)
[GCC 9.3.0] on GNU/linux
Type "help", "copyright", "credits" or "license" for more information.
>>> 3**4
81
>>> 2**6
64
>>> 2**5
32
>>> 3**3
27
4\12 (4 halfsteps of 12edo) functions as both 81/64 M3 and 5/4 vM3. The difference between the two is clouded through tempering of 81/80. Pay attention to the backs\ash in 4\12 as opposed to the forward s/ash in 5/4 and 81/64. Backs\ash is for e\os and forward s/ash for ra/ios. 4\12 is in between 5/4 vM3 and 81/64 M3. 9/7 ^M3 is not accessible in 12edo because it is too far away from 4\12. Similarly 27/22 is not accessible because it is also too far away. 12edo does not have enough notes to access these ratios from primes 7 and 11. 12edo has 81/64 M3 and 5/4 vM3, but it cannot chose between them. Tempering the comma 81/80 combines 81/64 M3 and 5/4 vM3 into just one note. 12edo represents these two intervals as 4\12.
41edo has enough notes to distinguish between M3 and vM3. 41edo can also access 9/7 ^M3 and 27/22 ~3. You can see how to translate between edos 41, 72, and 94 with the chart of 3rds below.
/ \12 \41 \72 \94
^M3 9/7 15\41 26\72 34\94
M3 81/64 14\41 24\72 32\94
4\12
vM3 5/4 13\41 23\72 30\94
~3 27/22 12\41 21\72 28\94
~3 11/9 12\41 21\72 27\94
^m3 6/5 11\41 19\72 25\94
3\12
m3 32/27 10\41 18\72 23/94
vm3 7/6 9\41 16\72 21\94
Violin
Kite guitar
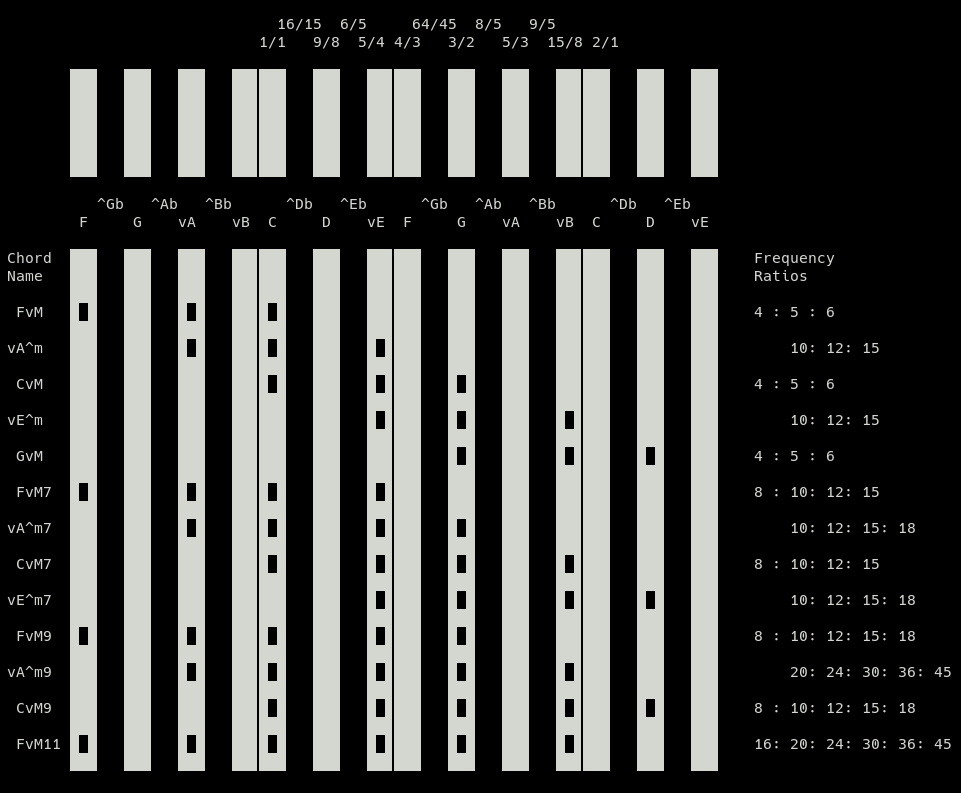
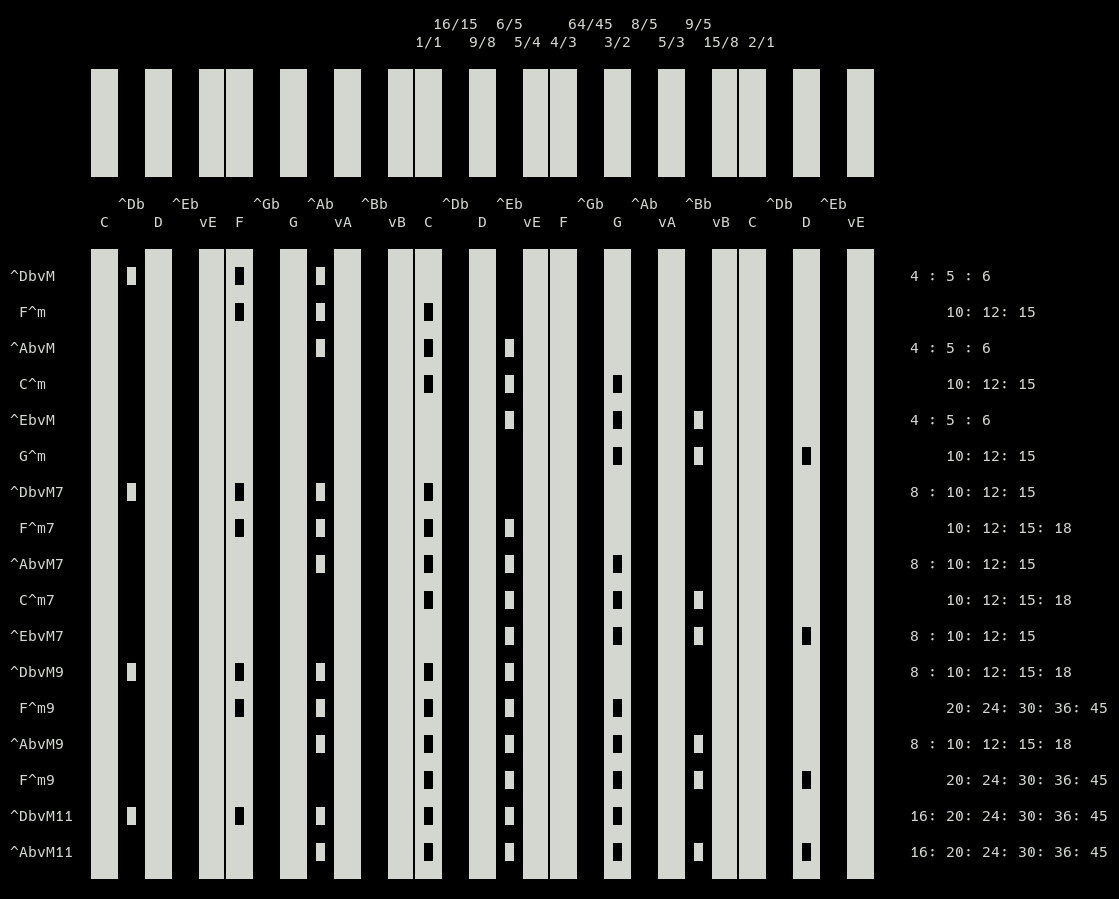
Chords of the harmonic series
About GNU/Linux Loves All
GNU/Linux Loves All is a project that makes microtonal music accessible through FLO software. Microtonal means anything beyond 12edo (standard tuning). Through microtonality, we can access the harmonic series and everything in between two notes. FLO stands for Free/Libre/Open. It means anything that respects and supports our Human Tech Rights. We can use FLO technology to be free to access the harmonic series and everything in between.
About FLO Software
What is FLO Software?
FLO (Free/Libre/Open) Software or Free Software is software that respects and supports a user's freedoms and Human Tech Rights. Proprietary software is built in such a way to ignore and exploit our Human Tech Rights.
What are our Human Tech Rights?
Every human has a right to
- privacy
- security
- repair
- internet
- education
- speech
Human Tech Rights and music technology should not be mutually exclusive
We can use GNU/Linux, the greatest operating system of all time, to make great music
What is GNU/Linux and what makes it the greatest operating system of all time?
GNU/Linux is a FLO operating system. It is FLO software licensed under the GNU General Public License, the greatest FLO software license of all time. GNU/Linux consistently out-paces proprietary alternatives in freedom, price, and functionality.
What is GNU?
GNU is a registered trademark owned by the Free Software Foundation. The FSF founder Richard Stallman created GNU, the GNU General Public Licenses, and the GNU Operating System (now known as GNU/Linux). GNU/Linux is more commonly known as Linux.